Estadistica inferencial.

http://matemath.com/azar/flash/camellos.swf

Estadistica inferencial.: CONCEPTOS BÁSICOS

Estadistica inferencial.: CONCEPTOS BÁSICOS

RECTA DE REGRESION

Empezamos intentando construir una función lineal de demanda. Suponga que su investigación de mercado muestra las siguientes estadísticas de venta para casas de varios precios durante el año pasado:

Precio (Miles de dólares)	160	180	200	220	240	260	280
Ventas de nueva casas este año	126	103	82	75	82	40	20

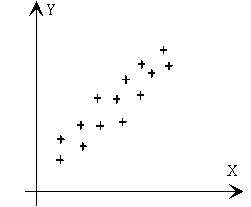
Queremos utilizar estos datos para construir una función de demanda para el mercado de los bienes raíces. (Recuerde que una función de demanda especifica la demanda, y, medida aquí por ventas anual, como una función del precio, x.) Aquí está una traza de y contra x:

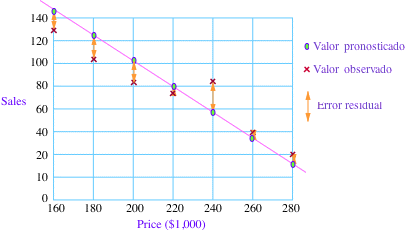
Los datos sugiera una recta, más o menos, y entonces una relación lineal entre y y x. Aquí son varias rectas que se acercan a los puntos:

Pregunta:  ¿Cuál recta ajusta los puntos lo más estrechamente que posible? 

Respuesta: Nos gustaría que las ventas que pronosticara la recta (los valores pronosticados ) estuvieran tan cerca como fuera posible de las ventas reales (los valores observados). Las diferencias entre los valores esperados y los valores pronosticados, que son los errores residuales, son las distancias verticales que se marcan in la figura más abajo.

Error residual = Valor observado - Valor pronosticado

INFERENCIA REGRESIÓN LINEAL

Se trata de predecir el comportamiento de Y usando X entonces el modelo de regresión lineal simple es de la forma:

Donde, Y es llamada la variable de respuesta o dependiente, X es llamada la variable predictora o independiente, α es el intercepto de la línea con el eje Y, β es la pendiente de la línea de regresión y ε es un error aleatorio, el cual se supone que tiene media 0 y varianza constante σ2

• Inferencia acerca de los coeficientes de regresión:

Las pruebas de hipótesis más frecuentes son, Ho: α = 0 versus

Ha: α ≠ 0 y

Ho: β = 0 versus Ha: β ≠ 0.

La prueba estadística para el caso de la pendiente viene dada por:

La cual se distribuye como una t con n-2 grados de libertad.

En estadística la regresión lineal o ajuste lineal es un método matemático que modela la relación entre una variable dependiente Y, las variables independientes Xi y un término aleatorio ε. Este modelo puede ser expresado como:

La regresión nos permite además, determinar el grado de dependencia de las series de valores X e Y, prediciendo el valor y estimado que se obtendría para un valor x que no esté en la distribución.

ORGANICEMOS LA INFORMACION

n1=100.n2=200 tamaño de la muestra 1 y 2

p1=0,2 y p2=0,5 proporción muestral que prefiere en cada población la modalidad a distancia

q1=0,8 y q2=0,5 proporción de muestra que prefiere otra modalidad

a=0,05 nivel de significación para probar la hipótesis

Pc=0,4 proporción combinada de la población que se determino favorable a la modalidad a distancia

Qc=0,6 proporción combinada de la población no favorable

PROBEMOS LA HIPÓTESIS

PASO  1, DEFINIR HIPÓTESIS:

PASO 2, DEFINIR NIVEL DE SIGNIFICACIÓN (a) y dibuje la región de rechazo en la curva normal estándar (curva Z): a = 0.05, Z = + 0,025 = + - 1,96

PASO 3, CALCULAR EL VALOR DE Z:

PASO 4, REGLA DE DECISIÓN:

No rechazar la hipótesis nula, si el valor calculado de Z cae entre - 1.96 y + 1.96. Rechazar la hipótesis nula y aceptar la hipótesis de investigación si Z no cae entre - 1.96 y + 1.96.

PASO 5, DECISIÓN:

Debido a que el valor calculado de Z ( -5.00) no cae entre los valores críticos (- 1.96 y + 1.96) se rechaza la hipótesis nula y se acepta que las preferencias por la modalidad de estudio varían según la edad del estudiante. En otras palabras, jóvenes y adultos no prefieren la modalidad a distancia en igual proporción.

EJEMPLO DE PRUEBA DE HIPÓTESIS

El consejo de universidades desea hacer un estudio sobre los gustos de la población adulta en cuanto a estudiar a distancia. Específicamente desea saber si la modalidad es exitosa entre la población joven y la madura.

Para ello se toman dos muestras independientes, una de jóvenes entre 21 y 30 años y otras de adultos mayores entre 31 y 40 años.

Se usara una encuesta simple entre cursantes de postgrado de varias especialidades en que se preguntara sobre la preferencia modal para que indiquen cual es el que le gusta mas.

PRUEBA DE HIPOTESIS

Una prueba de hipótesis consiste en contrastar dos hipótesis estadísticas. Tal contraste involucra la toma de decisión acerca de las hipótesis. La decisión consiste en rechazar o no una hipótesis en favor de la otra. Una hipótesis estadística se denota por “H” y son dos:- Ho: hipótesis nula
- H1: Hipótesis alternativa

HIPÓTESIS ALTERNATIVA: Al responder a un problema, es muy conveniente proponer otras hipótesis en que aparezcan variables independientes distintas de las primeras que formulamos. Por tanto, para no perder tiempo en búsquedas inútiles, es necesario hallar diferentes hipótesis alternativas como respuesta a un mismo problema y elegir entre ellas cuáles y en qué orden vamos a tratar su comprobación.

HIPÓTESIS NULA: La hipótesis nula es aquella que nos dice que no existen diferencias significativas entre los grupos.

Por ejemplo, supongamos que un investigador cree que si un grupo de jóvenes se somete a un entrenamiento intensivo de natación, éstos serán mejores nadadores que aquellos que no recibieron entrenamiento. Para demostrar su hipótesis toma al azar una muestra de jóvenes, y también al azar los distribuye en dos grupos: uno que llamaremos experimental, el cual recibirá entrenamiento, y otro que no recibirá entrenamiento alguno, al que llamaremos control. La hipótesis nula señalará que no hay diferencia en el desempeño de la natación entre el grupo de jóvenes que recibió el entrenamiento y el que no lo recibió.